KmPlot/da

Hjem » Programmer » Uddannelse » KmPlot

KmPlot er en matematisk funktionsplotter. Den er en del af KDE Education Project.

Nogle trigonometriske funktioner

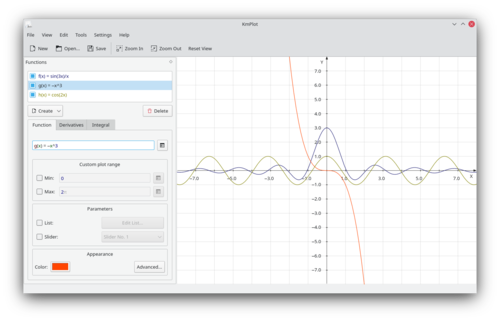
KmPlot har en stærk indbygget parser. Udprintninger med stor præcision er nyttige som arbejdsark i matematiktimerne.

Den kan plotte forskellige funktioner samtidigt og kombinere deres funktionsudtryk til at bygge nye funktioner. Den understøtter funktioner med parametre. Du kan ændre parametrene ved at bevæge en skyder og se, hvordan plottet ændres.

Hovedtræk

• stærk matematisk parser
• præcis udskrivning
• forskellige plottyper:
  • Cartesiske
  • parametriske
  • polære
  • implicitte
  • differentialligninger
• Meget konfigurerbart udseende (plotlinjer, akser, gitter)
• eksport til bitmat-formater (BMP og PNG) og skalerbar vektorgrafik (SVG).
• gem og indlæs hele sessioner i læsbart xml-format
• sporingstilstand: sigtekorn følger kurven, koordinaterne vises i statuslinjen
• understøtter zooming
• mulighed for at tegne 1. og 2. afledede og integralet af en funktion
• understøtter brugerdefinerede konstanter og parameterværdier
• forskellige værktøjer til funktioner:
  • find maksimums- og minimumspunkter
  • få y-værdien og tegn arealet mellem funktionen og y-aksen

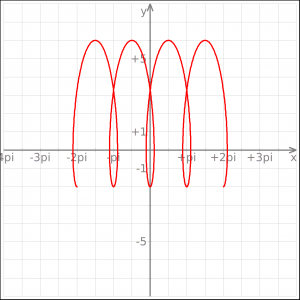
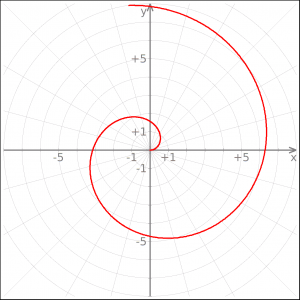
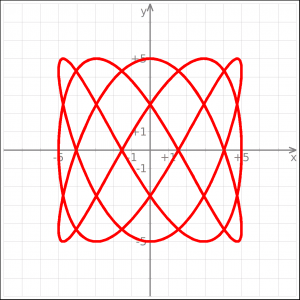
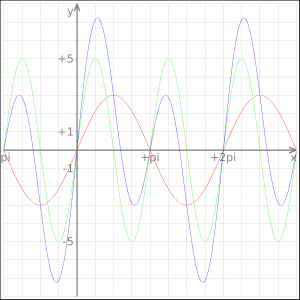
Eksempler på plots

x(t)=0.5(t-2sin t) y(t)=2(1-2cos t)	rf(x)=x
x(t)=5sin(3t) y(t)=3cos(5t)	f(x)=3sin x g(x)=5cos(2x-pi/2) h(x)=f(x)+g(x)

Mere detaljerede eksempler

• Brug af skydere

Dokumentation

• KmPlots håndbog