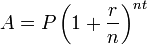KAlgebra/Credit payment: Difference between revisions
No edit summary |
No edit summary |
||
| (19 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
[[File:Compound_interest.svg.png|350px-Compound_interest.svg.png|right ]] | [[File:Compound_interest.svg.png|350px-Compound_interest.svg.png|right ]] | ||
Let's first recall what the compound interest is: | |||
'''Let's first recall what the compound interest is:''' | |||
Compound interest arises when interest is added to the principal, so that from that moment on, the interest that has been added also itself earns interest. This addition of interest to the principal is called compounding. A bank account, for example, may have its interest compounded every year: in this case, an account with $1000 initial principal and 20% interest per year would have a balance of $1200 at the end of the first year, $1440 at the end of the second year, and so on. | Compound interest arises when interest is added to the principal, so that from that moment on, the interest that has been added also itself earns interest. This addition of interest to the principal is called compounding. A bank account, for example, may have its interest compounded every year: in this case, an account with $1000 initial principal and 20% interest per year would have a balance of $1200 at the end of the first year, $1440 at the end of the second year, and so on. | ||
Formula for calculating compound interest: | '''Formula for calculating compound interest:''' | ||
[[File:Formula.png|200px]] | [[File:Formula.png|200px]] | ||
| Line 25: | Line 26: | ||
t = number of years | t = number of years | ||
Example usage: An amount of $ 1,500.00 a loan from the bank with an annual interest rate of 4.3 percent, which complicates the quarter. Find the value of the amount due after 6 years. | |||
A. Using the formula above, with P = 1500, r = 4.3/100 = 0.043, n = 4, and t = 6: | |||
[[File:3d67c3983b6c1b55bfa21cd8550ac0c7.png]] | |||
So, the value of the amount due after 6 years is approximately $1,938.op | |||
''Write all these functions in'' '''Console Mode''' | |||
'''1.This Function calculates the monthly interest rate by given yearly interest rate. | |||
''' | |||
{{Input|1=monthlyInterestRate:= yearlyInterestRate-> yearlyInterestRate/1200}} | {{Input|1=monthlyInterestRate:= yearlyInterestRate-> yearlyInterestRate/1200}} | ||
[[File:Screenshot0.png|600px]] | [[File:Screenshot0.png|600px]] | ||
2.This function calculates the monthly payment | '''2.This function calculates the monthly payment | ||
''' | |||
*mir=monthlyInterestRate | *mir=monthlyInterestRate | ||
| Line 41: | Line 52: | ||
[[File:Screenshot-1.png|600px]] | [[File:Screenshot-1.png|600px]] | ||
3.This Function calculates the whole amount you have to return to the bank | '''3.This Function calculates the whole amount you have to return to the bank''' | ||
{{Input|1=amount:=(monthlyPayment,months)->monthlyPayment*months}} | {{Input|1=amount:=(monthlyPayment,months)->monthlyPayment*months}} | ||
[[File:Screenshot02.png|600px]] | [[File:Screenshot02.png|600px]] | ||
== Sources used == | |||
* [http://en.wikipedia.org/wiki/Compound_interest Wikipedia] | |||
[[Category:Education]] | |||
Latest revision as of 16:43, 20 December 2010
This is tutorial how to calculate the compound interest with KAlgebra
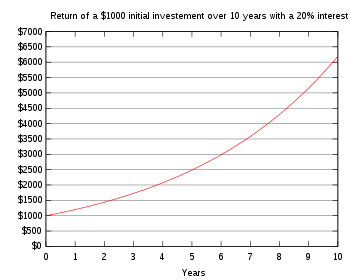
Let's first recall what the compound interest is:
Compound interest arises when interest is added to the principal, so that from that moment on, the interest that has been added also itself earns interest. This addition of interest to the principal is called compounding. A bank account, for example, may have its interest compounded every year: in this case, an account with $1000 initial principal and 20% interest per year would have a balance of $1200 at the end of the first year, $1440 at the end of the second year, and so on.
Formula for calculating compound interest:
Where,
A = final amount
P = principal amount (initial investment)
r = annual nominal interest rate (as a decimal)
n = number of times the interest is compounded per year(12 times)
t = number of years
Example usage: An amount of $ 1,500.00 a loan from the bank with an annual interest rate of 4.3 percent, which complicates the quarter. Find the value of the amount due after 6 years.
A. Using the formula above, with P = 1500, r = 4.3/100 = 0.043, n = 4, and t = 6:
So, the value of the amount due after 6 years is approximately $1,938.op
Write all these functions in Console Mode
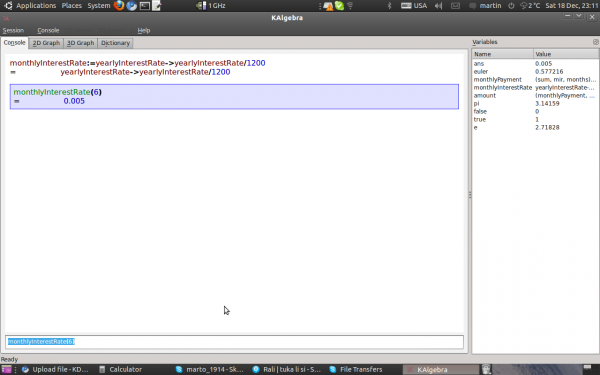
1.This Function calculates the monthly interest rate by given yearly interest rate.
monthlyInterestRate:= yearlyInterestRate-> yearlyInterestRate/1200
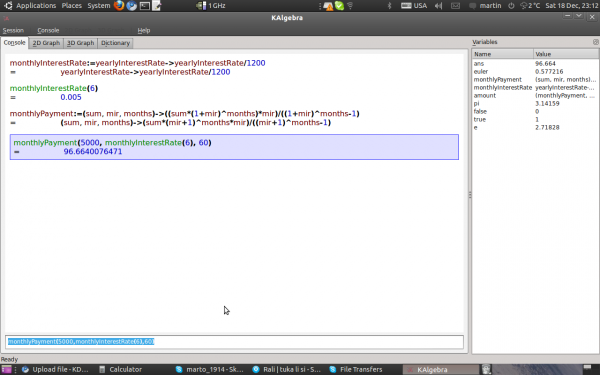
2.This function calculates the monthly payment
- mir=monthlyInterestRate
monthlyPayment:=(sum, mir, months)->(sum*(1+mir)^months*mir)/((1+mir)^months-1)
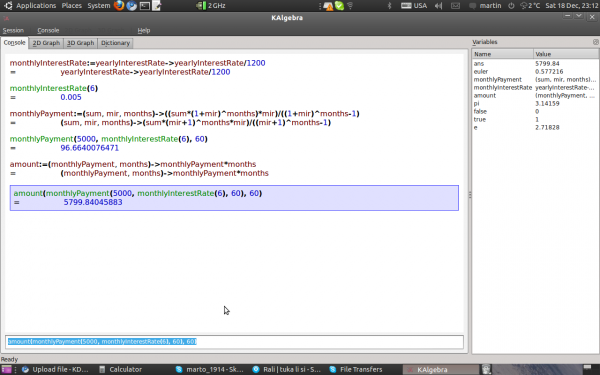
3.This Function calculates the whole amount you have to return to the bank
amount:=(monthlyPayment,months)->monthlyPayment*months