KAlgebra/Console Tab/da: Difference between revisions
Importing a new version from external source |
No edit summary |
||
| (34 intermediate revisions by 2 users not shown) | |||
| Line 26: | Line 26: | ||
=== Hjælp! (eller er det Hjælp?) === | === Hjælp! (eller er det Hjælp?) === | ||
Ordbogen er den bedste kilde til alle '''KAlgebras''' funktioner. Du klikker blot på fanebladet '''Ordbog''', så får du en liste med alle 64 funktioner. Hvis du vil redigere værdien af en variabel, så kan du dobbeltklikke på den aktuelle værdi i variabellisten og skrive hvad du vil. '''KAlgebra''' har en autofuldførelses-funktion, som du kan bruge i dine beregninger. Den aktiveres når du begynder at skrive i indtastningslinjen. Efter at have skrevet mindst et bogstav vil den give dig nogle valgmuligheder, som du måske ønsker at skrive. Hvis en af disse valgmuligheder er passende, så klik på den for at få færdiggjort det du var ved at skrive. | |||
=== | === Det ultimative eksempel på matematisk geekeri === | ||
For at vise nogle af '''KAlgebras''' konsolfunktioner vil vi finde arealet under en sinuskurve. For at gøre det vil vi estimere arealet som arealet af en række trapezoider, som passer under sinuskurven. Til at begynde med definerer vi en funktion (f), som giver sinuskurven fra 0 til 3,14 radianer: | |||
{{Input|1=<nowiki>f:=x->sin(x)</nowiki>}} | {{Input|1=<nowiki>f:=x->sin(x)</nowiki>}} | ||
Vi havde ikke behøvet at gøre dette, vi kunne bare bruge sin(x) direkte, men nu kan vi erstatte sin(x) i definitionen af f, sådan at vi kan finde arealet af andre interessante former. | |||
Herefter definerer vi en funktion, som kan beregne arealet af et trapezoid: | |||
{{Input|1=nowiki>A:=(b,h1,h2)->0.5*(h1+h2)*b</nowiki>}} | {{Input|1=<nowiki>A:=(b,h1,h2)->0.5*(h1+h2)*b</nowiki>}} | ||
Ovenstående funktion har tre variable (basis, højde 1 og højde 2), hvilket '''KAlgebra''' håndterer uden problemer. | |||
Dernæst skal vi beregne er række af trapezoider under sinuskurven i skridt af 0,01 radianer. Til at hjælpe med det definerer vi funktionen x(k)=0,01k eller: | |||
{{Input|1=<nowiki>x:=k->0.01*k</nowiki>}} | {{Input|1=<nowiki>x:=k->0.01*k</nowiki>}} | ||
Når k nu tæller fra o til 314, så ændres x fra 0 til 3,14 radianer. Vi summerer trapezoid-arealerne op ved brug af funktionen sum: | |||
{{Input|1=<nowiki>sum(A(.01,f(x(k)),f(x(k+1))): k=0..314)</nowiki>}} | {{Input|1=<nowiki>sum(A(.01,f(x(k)),f(x(k+1))): k=0..314)</nowiki>}} | ||
Dette viser meget af '''KAlgebras''' egenskaber og syntaks. Du kan se, hvordan man bruger den indbyggede funktion sum. Vi demonstrerer brug af funktioner i funktioner. Vi ser også syntaksen for sekvenser. | |||
[[File:Kalgebra-sinearea-example.png]] | [[File:Kalgebra-sinearea-example.png]] | ||
Vort svar er meget tæt på to, hvilket faktisk er det eksakte svar. | |||
=== | === Rekursion === | ||
Se, rekursion. | |||
O.k., for rigtigt at forstå rekursion skal du først forstå rekursion. '''KAlgebras''' konsol giver brugeren et virtuelt laboratorium til at eksperimentere med og bruge rekursion. Formentlig det mest brugte eksempel på rekursion er fakultet-funktionen. Herunder definerer vi vores egen fakultet-funktion ved brug af '''KAlgebras''' evne til at definere funktioner, udføre logik inde i funktioner og få funktioner til at kalde sig selv, hvilket er definitionen på rekursion: | |||
{{Input|1=<nowiki>fact:=n->piecewise{ n<=1 ? 1, ? n*fact(n-1)}</nowiki>}} | {{Input|1=<nowiki>fact:=n->piecewise{ n<=1 ? 1, ? n*fact(n-1)}</nowiki>}} | ||
Analyserer vi det, så har vi defineret vores egen funktion, fact, som tilfældigvis kalder funktionen fact. Dette udnytter den rekursive definition af fakultet-funktionen. | |||
fact(n) = n! = n*(n-1)*(n-2)*...*2*1 | fact(n) = n! = n*(n-1)*(n-2)*...*2*1 | ||
Bemærk, at (n-1)! = (n-1)*(n-2)*...*2*1, | |||
vi har så: n! = n*(n-1)! | |||
or fact(n) = n*fact(n-1) | or fact(n) = n*fact(n-1) | ||
For at afbryde kæden af beregninger definerer vi, at 1! = 1. Vi udtrykker denne smule logik med konstruktionen piecewise{ udtryk ? værdi, udtryk ? værdi, ..., ? standardværdi }. | |||
[[File:Kalgebra-recursion-example.png]] | [[File:Kalgebra-recursion-example.png]] | ||
=== | === Sjov med lister === | ||
Fra version 0.11 leveres '''KAlgebra''' med avancerede (og med avanceret mener jeg tidsbesparende) operationer på lister. '''KAlgebra''' havde tidligere en måde at definere en liste af variable eller værdier. For eksempel kunne man definere en liste med tal således: | |||
{{Input|1=<nowiki>x:=list{0,.2,.4,.6,.8,1,1.2,1.4,1.6,1.8,2,2.2,2.4,2.6,2.8,3.0,3.2}</nowiki>}} | {{Input|1=<nowiki>x:=list{0,.2,.4,.6,.8,1,1.2,1.4,1.6,1.8,2,2.2,2.4,2.6,2.8,3.0,3.2}</nowiki>}} | ||
Nu har '''KAlgebra''' funktionen ''map'', som giver brugeren mulighed for at anvende en funktion på hvert element i listen. Som et enkelt eksempel kunne man beregne sinus af hvert element i listen. Man kunne være fristet til at skrive '''sin(x)'''. Man ville så blive skuffet. | |||
For at anvende en funktion på hvert element i listen bruger vi funktionen map således: | |||
{{Input|1=<nowiki>s := map( u->sin(u), x)</nowiki>}} | {{Input|1=<nowiki>s := map( u->sin(u), x)</nowiki>}} | ||
Det første argument til funktionen map angiver den funktion, der skal anvendes på alle elementerne i den liste, der gives som det andet argument. Nu er '''s''' altså en liste, der indeholder sinusværdierne af hvert element i x. | |||
Hvis vi vil at begrænse antallet af elementer i en liste kan vi bruge funktionen filter til at udvælge de elementer, vi vil beholde i listen. | |||
{{Input|1=<nowiki>f := filter( u-> and(u>=-0.5,u<=0.5), s)</nowiki>}} | {{Input|1=<nowiki>f := filter( u-> and(u>=-0.5,u<=0.5), s)</nowiki>}} | ||
Efter dette vil f kun indeholde de elementer fra s, som ligger imellem -0,5 og 0,5. Det første argument til funktionen filter angiver en logisk funktion, som bruges til at udvælge de værdier i listen, som vi vil have. | |||
Herunder er et skærmbillede med de forskellige listeoperationer, som vi har omtalt: | |||
[[File:Kalgebra-listopsoxy-example.png]] | [[File:Kalgebra-listopsoxy-example.png]] | ||
=== | === Afsluttende ord === | ||
Vi har kun kradset i overfladen af de fantastiske ting, som kan laves i '''KAlgebras''' konsol. Der er masser at ting, som kan gøres, så rul ærmerne op og lav noget matematik! | |||
--[[User:Trlanzi|trLanzi]] 01:10, 1 | --[[User:Trlanzi|trLanzi]] 01:10, 1. december 2011 (UTC) | ||
[[Category: | [[Category:Uddannelse/da]] | ||
[[Category: | [[Category:Vejledning/da]] | ||
Latest revision as of 15:14, 5 January 2013
Lær konsollen at kende
KAlgebras faneblad Konsol er det første du ser, når du åbner KAlgebra. Det er som en regnemaskine, bare meget bedre. Den lille redigeringslinje helt nederst i vinduet er indtastningslinjen. Den bruges til at indskrive det problem, du vil have løst. Svaret kommer i visningsområdet i midten af vinduet. I højre side er der endnu et vindue, Variabler. Det viser den aktuelle værdi af variablerne så som pi, true, false og selv det aktuelle svar. Konsollen kan bruges til at lave simple og komplekse beregninger, og det er nemmere og hurtigere end at starte et lommeregner-program. For at udføre en beregning skriver du den ligning du vil have løst i indtastningslinjen. Efter at have tastet Enter vises svaret i visningsområdet
Lig med! eller Lig med? det er spørgsmålet
En af de vigtigste ting i KAlgebra er at kende forskel på "lig med!" og "lig med?" Jeg ved hvad du tænker, "Hvad er forskellen?". Jo, "lig med!" (:=) bruges til at sætte eller definere værdien af den valgte variabel. Med y:=3 defineres for eksempel y til at have værdien 3. "Lig med?" (=) betyder, at du spørger om en variable er lig med en værdi eller ej. Du vil så enten få svaret true (sandt) eller false (falsk). Hvis du for eksempel indtaster y:=3 og derefter y=2, så får du svaret “false”. Altså er := den operator, som KAlgebra bruger til at definere og = er den logiske operator (ligesom <, >, <= og >=).
KAlgebra som en hurtigere regnemaskine
Der er også almindelige regnemaskine-funktioner så som addition (+), subtraktion (-), multiplikation (*), division (/), eksponent (** og ^) samt paranteser () til at styre rækkefølgen. Hvis du vil tage kvadratroden af et tal, så skriver du tallet fulgt af ^0.5. For eksempel findes kvadratroden af 25 ved: 25^0.5. Hvis du skulle bruge et lommeregner-program på computeren, så skulle du muse rundt til de forskellige virtuelle taster. I KAlgebras konsol kan du blot skrive, hvad du vil beregne, hvilket er meget hurtigere og mere direkte.
Definition af brugerfunktioner med lambda-operatoren
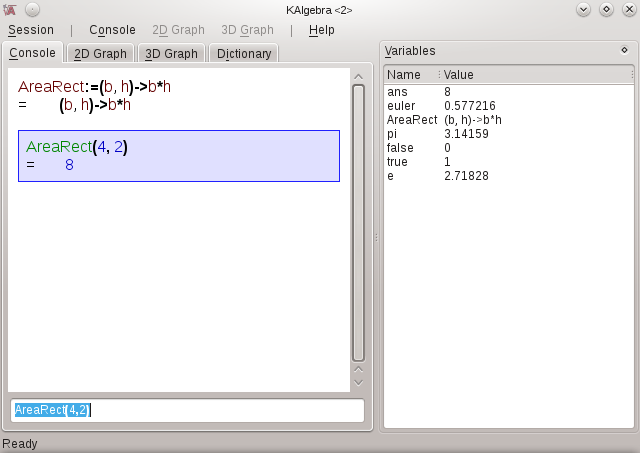
Lambda-operatoren er svær at forstå ved første øjekast. Enkelt sagt er det KAlgebras måde at definere en ny funktion i konsollen. Den bedste måde at diskutere, hvordan den bruges er igennem et eksempel. Til at beregne arealet af et rektangel kunne vi for eksempel definere:
AreaRect:=(b,h)->b*h
Det jeg gjorde her var at definere (:=) funktionen AreaRect. AreaRect er en funktion i to frie variable, b og h (basis og højde). Lambda-operatoren (->) viser, hvordan de afbildes over i arealet af et rektangel. Efter at have indtastet denne definition er funktionen AreaRect bygget ind i KAlgebra. Prøv den bare, skriv for eksempel AreaRect(4,2); du vil få svaret 8.
Herunder ses et skærmbillede, som viser definitionen af denne meget enkle funktion, hvordan den vises i variabellisten og bruges af brugeren med resultatet vist i displayet.
Hjælp! (eller er det Hjælp?)
Ordbogen er den bedste kilde til alle KAlgebras funktioner. Du klikker blot på fanebladet Ordbog, så får du en liste med alle 64 funktioner. Hvis du vil redigere værdien af en variabel, så kan du dobbeltklikke på den aktuelle værdi i variabellisten og skrive hvad du vil. KAlgebra har en autofuldførelses-funktion, som du kan bruge i dine beregninger. Den aktiveres når du begynder at skrive i indtastningslinjen. Efter at have skrevet mindst et bogstav vil den give dig nogle valgmuligheder, som du måske ønsker at skrive. Hvis en af disse valgmuligheder er passende, så klik på den for at få færdiggjort det du var ved at skrive.
Det ultimative eksempel på matematisk geekeri
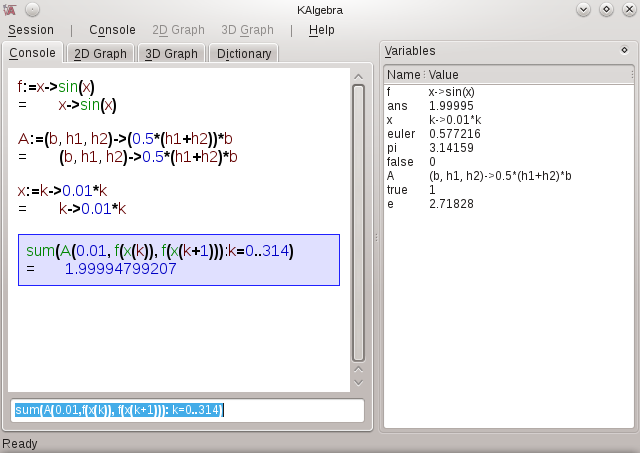
For at vise nogle af KAlgebras konsolfunktioner vil vi finde arealet under en sinuskurve. For at gøre det vil vi estimere arealet som arealet af en række trapezoider, som passer under sinuskurven. Til at begynde med definerer vi en funktion (f), som giver sinuskurven fra 0 til 3,14 radianer:
f:=x->sin(x)
Vi havde ikke behøvet at gøre dette, vi kunne bare bruge sin(x) direkte, men nu kan vi erstatte sin(x) i definitionen af f, sådan at vi kan finde arealet af andre interessante former.
Herefter definerer vi en funktion, som kan beregne arealet af et trapezoid:
A:=(b,h1,h2)->0.5*(h1+h2)*b
Ovenstående funktion har tre variable (basis, højde 1 og højde 2), hvilket KAlgebra håndterer uden problemer.
Dernæst skal vi beregne er række af trapezoider under sinuskurven i skridt af 0,01 radianer. Til at hjælpe med det definerer vi funktionen x(k)=0,01k eller:
x:=k->0.01*k
Når k nu tæller fra o til 314, så ændres x fra 0 til 3,14 radianer. Vi summerer trapezoid-arealerne op ved brug af funktionen sum:
sum(A(.01,f(x(k)),f(x(k+1))): k=0..314)
Dette viser meget af KAlgebras egenskaber og syntaks. Du kan se, hvordan man bruger den indbyggede funktion sum. Vi demonstrerer brug af funktioner i funktioner. Vi ser også syntaksen for sekvenser.
Vort svar er meget tæt på to, hvilket faktisk er det eksakte svar.
Rekursion
Se, rekursion.
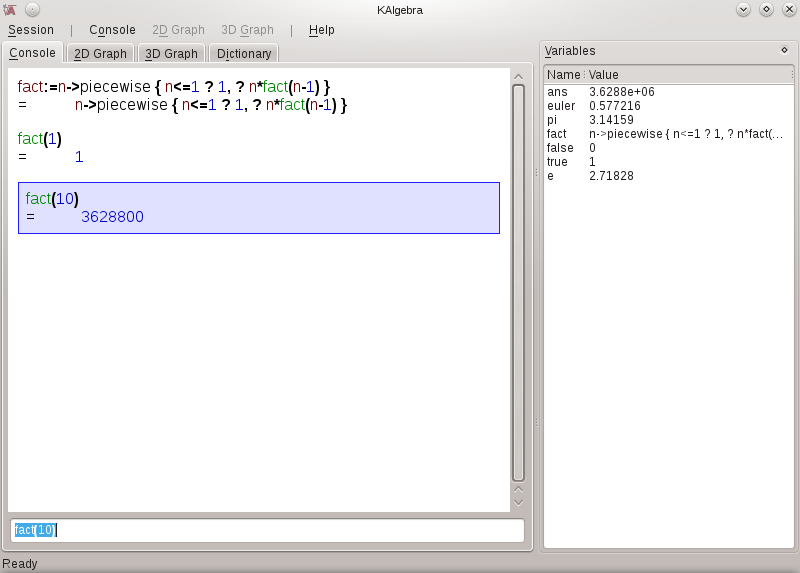
O.k., for rigtigt at forstå rekursion skal du først forstå rekursion. KAlgebras konsol giver brugeren et virtuelt laboratorium til at eksperimentere med og bruge rekursion. Formentlig det mest brugte eksempel på rekursion er fakultet-funktionen. Herunder definerer vi vores egen fakultet-funktion ved brug af KAlgebras evne til at definere funktioner, udføre logik inde i funktioner og få funktioner til at kalde sig selv, hvilket er definitionen på rekursion:
fact:=n->piecewise{ n<=1 ? 1, ? n*fact(n-1)}
Analyserer vi det, så har vi defineret vores egen funktion, fact, som tilfældigvis kalder funktionen fact. Dette udnytter den rekursive definition af fakultet-funktionen.
fact(n) = n! = n*(n-1)*(n-2)*...*2*1
Bemærk, at (n-1)! = (n-1)*(n-2)*...*2*1, vi har så: n! = n*(n-1)! or fact(n) = n*fact(n-1)
For at afbryde kæden af beregninger definerer vi, at 1! = 1. Vi udtrykker denne smule logik med konstruktionen piecewise{ udtryk ? værdi, udtryk ? værdi, ..., ? standardværdi }.
Sjov med lister
Fra version 0.11 leveres KAlgebra med avancerede (og med avanceret mener jeg tidsbesparende) operationer på lister. KAlgebra havde tidligere en måde at definere en liste af variable eller værdier. For eksempel kunne man definere en liste med tal således:
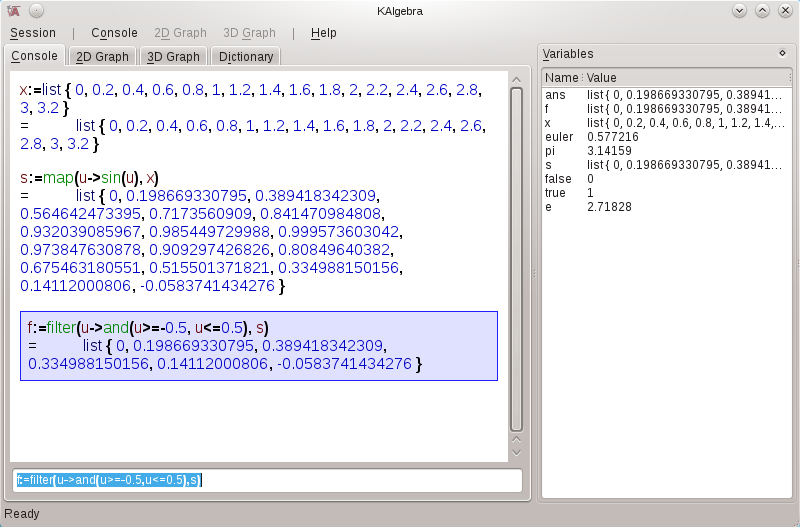
x:=list{0,.2,.4,.6,.8,1,1.2,1.4,1.6,1.8,2,2.2,2.4,2.6,2.8,3.0,3.2}
Nu har KAlgebra funktionen map, som giver brugeren mulighed for at anvende en funktion på hvert element i listen. Som et enkelt eksempel kunne man beregne sinus af hvert element i listen. Man kunne være fristet til at skrive sin(x). Man ville så blive skuffet.
For at anvende en funktion på hvert element i listen bruger vi funktionen map således:
s := map( u->sin(u), x)
Det første argument til funktionen map angiver den funktion, der skal anvendes på alle elementerne i den liste, der gives som det andet argument. Nu er s altså en liste, der indeholder sinusværdierne af hvert element i x.
Hvis vi vil at begrænse antallet af elementer i en liste kan vi bruge funktionen filter til at udvælge de elementer, vi vil beholde i listen.
f := filter( u-> and(u>=-0.5,u<=0.5), s)
Efter dette vil f kun indeholde de elementer fra s, som ligger imellem -0,5 og 0,5. Det første argument til funktionen filter angiver en logisk funktion, som bruges til at udvælge de værdier i listen, som vi vil have.
Herunder er et skærmbillede med de forskellige listeoperationer, som vi har omtalt:
Afsluttende ord
Vi har kun kradset i overfladen af de fantastiske ting, som kan laves i KAlgebras konsol. Der er masser at ting, som kan gøres, så rul ærmerne op og lav noget matematik!
--trLanzi 01:10, 1. december 2011 (UTC)