KmPlot: Difference between revisions
Pipesmoker (talk | contribs) No edit summary |
Pipesmoker (talk | contribs) (example plots added) |
||
| Line 20: | Line 20: | ||
* ability to draw the 1st and 2nd derivative and the integral of a plot function | * ability to draw the 1st and 2nd derivative and the integral of a plot function | ||
* support user defined constants and parameter values | * support user defined constants and parameter values | ||
* various tools for plot functions: find minium/maximum point | * various tools for plot functions: | ||
**find minium/maximum point | |||
**get y-value and draw the area between the function and the y-axis | |||
==Example Plots== | |||
{|style="width:500px" cellpadding="5" | |||
| [[Image:kmplot_cycloide.png|thumb|230px|center]] | |||
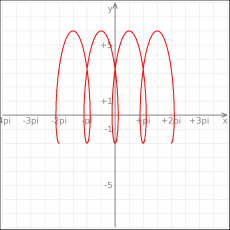
:x(t)=0.5(t-2sin t) | |||
:y(t)=2(1-2cos t) | |||
|| [[Image:kmplot_spiral.png|thumb|230px|center]] | |||
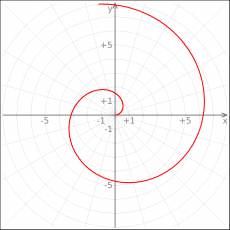
:rf(x)=x | |||
|- | |||
| [[Image:kmplot_lisajou.png|thumb|230px|center]] | |||
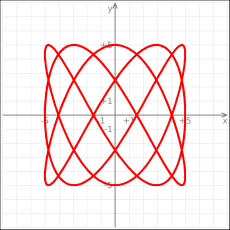
:x(t)=5sin(3t) | |||
:y(t)=3cos(5t) | |||
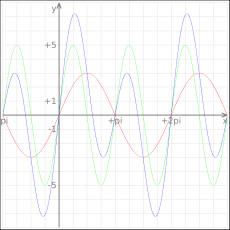
|| [[Image:kmplot_sum_of_functions.png|thumb|230px|center]] | |||
:f(x)=3sin x | |||
:g(x)=5cos(2x-pi/2) | |||
:h(x)=f(x)+g(x) | |||
|} | |||
[[Category:Education]] | [[Category:Education]] | ||
Revision as of 06:35, 31 May 2010

Under Construction
This is a new page, currently under construction!
Template:I18n/Language Navigation Bar
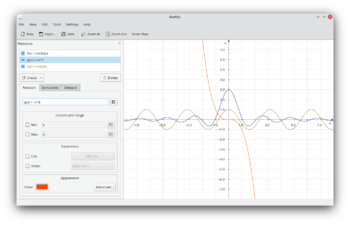 |
KmPlot is a mathematical function plotter. |
Features
- powerful mathematical parser
- precise metric printing
- different plot types (functions, parametric, polar)
- highly configurable visual settings (plot line, axes, grid)
- export to bitmap format (BMP and PNG) and scalable vector graphics (SVG)
- save/load complete session in readable xml format
- trace mode: cross hair following plot, coordinates shown in the status bar
- support zooming
- ability to draw the 1st and 2nd derivative and the integral of a plot function
- support user defined constants and parameter values
- various tools for plot functions:
- find minium/maximum point
- get y-value and draw the area between the function and the y-axis
Example Plots
|
|
|
|
