KAlgebra/Console Tab/da

Lær konsollen at kende

KAlgebras faneblad Konsol er det første du ser, når du åbner KAlgebra. Det er som en regnemaskine, bare meget bedre. Den lille redigeringslinje helt nederst i vinduet er indtastningslinjen. Den bruges til at indskrive det problem, du vil have løst. Svaret kommer i visningsområdet i midten af vinduet. I højre side er der endnu et vindue, Variabler. Det viser den aktuelle værdi af variablerne så som pi, true, false og selv det aktuelle svar. Konsollen kan bruges til at lave simple og komplekse beregninger, og det er nemmere og hurtigere end at starte et lommeregner-program. For at udføre en beregning skriver du den ligning du vil have løst i indtastningslinjen. Efter at have tastet Enter vises svaret i visningsområdet

Lig med! eller Lig med? det er spørgsmålet

En af de vigtigste ting i KAlgebra er at kende forskel på "lig med!" og "lig med?" Jeg ved hvad du tænker, "Hvad er forskellen?". Jo, "lig med!" (:=) bruges til at sætte eller definere værdien af den valgte variabel. Med y:=3 defineres for eksempel y til at have værdien 3. "Lig med?" (=) betyder, at du spørger om en variable er lig med en værdi eller ej. Du vil så enten få svaret true (sandt) eller false (falsk). Hvis du for eksempel indtaster y:=3 og derefter y=2, så får du svaret “false”. Altså er := den operator, som KAlgebra bruger til at definere og = er den logiske operator (ligesom <, >, <= og >=).

KAlgebra som en hurtigere regnemaskine

Der er også almindelige regnemaskine-funktioner så som addition (+), subtraktion (-), multiplikation (*), division (/), eksponent (** og ^) samt paranteser () til at styre rækkefølgen. Hvis du vil tage kvadratroden af et tal, så skriver du tallet fulgt af ^0.5. For eksempel findes kvadratroden af 25 ved: 25^0.5. Hvis du skulle bruge et lommeregner-program på computeren, så skulle du muse rundt til de forskellige virtuelle taster. I KAlgebras konsol kan du blot skrive, hvad du vil beregne, hvilket er meget hurtigere og mere direkte.

Definition af brugerfunktioner med lambda-operatoren

Lambda-operatoren er svær at forstå ved første øjekast. Enkelt sagt er det KAlgebras måde at definere en ny funktion i konsollen. Den bedste måde at diskutere, hvordan den bruges er igennem et eksempel. Til at beregne realet af et rektangel kunne vi for eksempel definere:

AreaRect:=(b,h)->b*h 

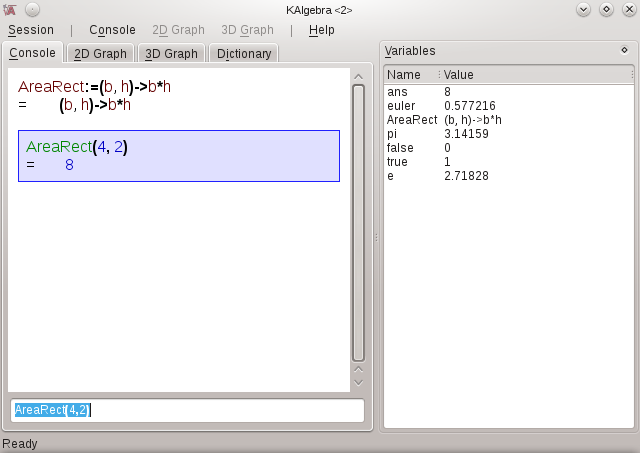
Det jeg gjorde her var at definere (:=) funktionen AreaRect. AreaRect er en funktion i to frie variable, b og h (basis og højde). Lambda-operatoren (->) viser, hvordan de afbildes over i arealet af et rektangel. Efter at have indtastet denne definition er funktionen AreaRect bygget ind i KAlgebra. Prøv den bare, skriv for eksempel AreaRect(4,2); du vil få svaret 8.

Herunder ses et skærmbillede, som viser definitionen af denne meget enkle funktion, hvordan den vises i variabellisten og bruges af brugeren med resultatet vist i displayet.

Hjælp! (eller er det Hjælp?)

The dictionary is the best source for all of KAlgebra's available functions. You just click the dictionary tab, and you will get a list of all 64 functions. If you want to edit the value of a variable, you can double click on the current value in the variables list and enter anything you want. KAlgebra includes an auto complete feature which will suggest possible functions you may use for your calculations. It starts working when you begin typing in the input bar. Once you type in at least one letter, it will give you several options as to what you may want to enter. If one of those options is suitable, you click on it, and what you've been typing will be automatically completed.

The Ultimate Example of Math Geekery

To show some of the KAlgebra console concepts, we would like to find the area under a sine curve. To do so, we are going to estimate the area as the area of a bunch of trapezoids that fit under the sine curve. For starters, we define a function (f) that provides our sine curve from 0 to 3.14 radians:

f:=x->sin(x)

We didn't have to do this, we could just use sin(x) directly, but we can also replace sin(x) in the definition of f to find the area of other interesting shapes.

Next we define a function that is able to calculate the area of a trapezoid:

nowiki>A:=(b,h1,h2)->0.5*(h1+h2)*b</nowiki>

The above function is a function of three variables (base, height 1, and height 2) that KAlgebra is more than capable of handling.

Next, we are going to evaluate the series of trapezoids beneath the sine curve in increments of 0.01 radians. To help us do this, we define a helper function x(k)=0.01*k or:

x:=k->0.01*k

So that as k counts from 0 to 314, x changes from 0 to 3.14 radians. We sum the trapezoid areas up using sum function:

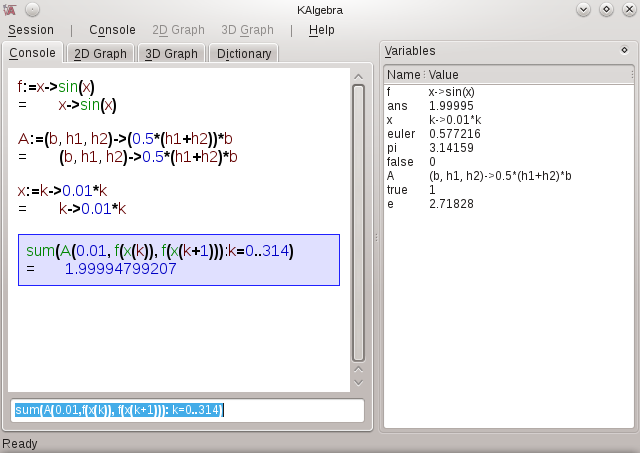
sum(A(.01,f(x(k)),f(x(k+1))): k=0..314)

This shows off a lot of KAlgebra's capabilities and syntax. You can see the use of the built in function, sum. We show off the use of nested functions. Also, we see the use of the range syntax.

Our answer is very close to two, which happens to be the exact solution.

Recursion

See, Recursion.

OK, seriously, to understand recursion, you must first understand recursion. The KAlgebra console provides the user with a virtual laboratory for experimenting with and using recursion. Probably the most used example of recursion is the factorial. Below we define our own factorial function using KAlgebra's capabilities for defining functions, performing logic inside of functions, and having a function call itself, which is the definition of recursion:

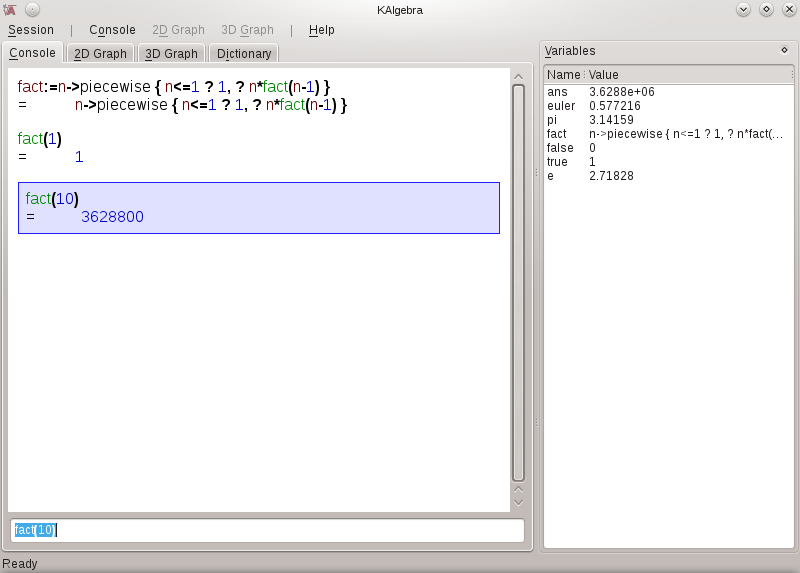
fact:=n->piecewise{ n<=1 ? 1, ? n*fact(n-1)}

So, breaking this down, we're defining our own function (fact) which just so happens to call fact. This takes advantage of the recursive definition of the factorial function.

fact(n) = n! = n*(n-1)*(n-2)*...*2*1

Noting that (n-1)! = (n-1)*(n-2)*...*2*1, we have: n! = n*(n-1)! or fact(n) = n*fact(n-1)

To stop the chain of calculations, we define that 1! = 1. We accomplish this bit of logic using the piecewise{ expression ? value, expression ? value, ..., ? default value} construct.

Fun with Lists

Beginning with version 0.11, KAlgebra comes with advanced (and by advanced, I mean time saving) list operations. KAlgebra had previously come with the means of entering a list of variables or values. For example, one could enter a list of numbers as follows:

x:=list{0,.2,.4,.6,.8,1,1.2,1.4,1.6,1.8,2,2.2,2.4,2.6,2.8,3.0,3.2}

Now, with the map function, KAlgebra provides the user with the means of applying a function to each element of the list. As a simple example, one might wish to evaluate the sine of each element of the list. One might also be tempted to enter sin(x). One would be disappointed.

To apply a function to each element of the list we use the map function as follows:

s := map( u->sin(u), x)

The first argument of the map function sets up the function that will be applied to all elements of the list given in the second argument of the map function. So now, s is a list holding the sine of every element of x.

If we want to pare down a list we can use the filter function to select the list elements we want to keep:

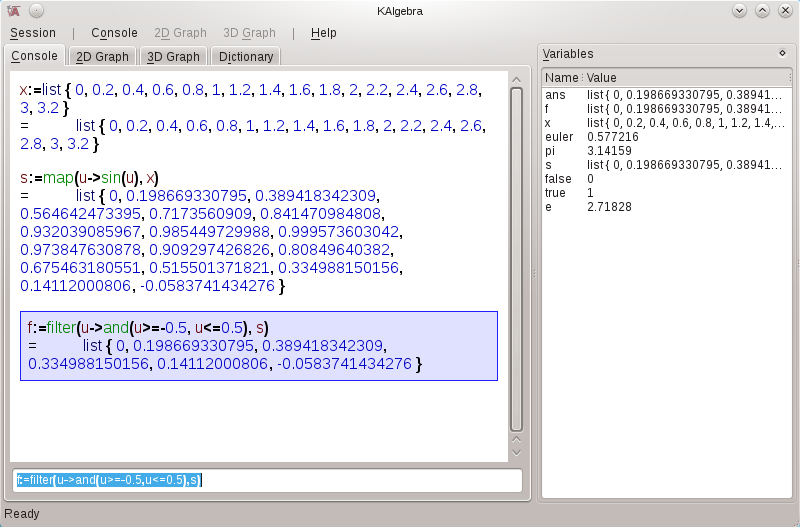
f := filter( u-> and(u>=-0.5,u<=0.5), s)

After this, f will contain only elements of s that are between -0.5 and +0.5. The first argument of the filter function defines a logical operation used to select the values of the list that we want.

Below is a screenshot of the various list operations discussed:

Parting Words

We have scratched the surface of the wonders presented by the KAlgebra user console. There is a lot of stuff that can be done, so roll up your sleeves, and do some math!

--trLanzi 01:10, 1 December 2011 (UTC)