LabPlot/ComputationalNotebooks: Difference between revisions
update info |
No edit summary |
||
| Line 32: | Line 32: | ||
With this, powerful calculations carried out inside of different CAS environments can be combined with the user-friendly visualization and editing capabilities of LabPlot. | With this, powerful calculations carried out inside of different CAS environments can be combined with the user-friendly visualization and editing capabilities of LabPlot. | ||
[[File:Labplot2 appdata 03.png|frameless|center|upright=3.0]] | [[File:Labplot2 appdata 03.png|frameless|center|upright=3.0]] | ||
Maxima session exploring the chaotic dynamics of the Duffing oscillator. The forced oscillator's differential equation is solved using Maxima, and the results are visualized using LabPlot. Plots include the oscillator's trajectory, phase space, and Poincaré map, showcasing the system's complex behavior. | |||
[[File:Python session.png|frameless|center|upright=3.0]] | [[File:Python session.png|frameless|center|upright=3.0]] | ||
Python session analyzing the effect of Blackman windowing on the Fourier transform. It demonstrates how windowing can enhance the clarity of frequency components in signal processing, with plots showing the Fourier transform before and after applying the Blackman window. | |||
=== See Also === | === See Also === | ||
Revision as of 00:11, 1 March 2024
LabPlot/ComputationalNotebooks
LabPlot's Computational Notebooks offer an interactive and animated interface to powerful mathematics and statistics packages as well as programming languages. These include Maxima, Octave, R, Scilab, Sage, KAlgebra, Qalculate!, Python, Julia, and Lua. This integration enables seamless execution of computations and immediate visualization of results within the same environment, providing a user-friendly interface for complex calculations and data analysis.
Key Features
- Multi-Language and CAS Support: LabPlot supports a wide range of programming languages and CAS, empowering users to utilize the computational capabilities of Maxima, Octave, R, Scilab, Sage, KAlgebra, Qalculate!, Python, Julia, and Lua within the same notebook.
- Simultaneous Notebooks and Languages: Users can work with multiple notebooks and languages simultaneously, facilitating a flexible workflow adaptable to various computational requirements.
- Array-like Data as Plot Sources: LabPlot recognizes notebook variables containing array-like data (e.g., Maxima lists, Python lists and tuples, Julia vectors and tuples) and permits selecting them as sources for interactive plots, simplifying plot creation by utilizing computation outputs directly.
- Extensive Edition Capabilities: The notebook interface offers extensive editing capabilities, enabling users to perform complex manipulations and analyses on their data directly within the notebook.
- Plotting Support: LabPlot provides robust support for plotting, enabling users to create a wide range of plots and charts directly within the notebook interface.
- Markdown and LaTeX Syntax: Users can utilize Markdown and LaTeX syntax within the notebooks to create richly formatted text, equations, and documentation alongside their computations and visualizations.
- Compatibility with Jupyter and Cantor Projects: LabPlot can read Jupyter and Cantor projects, allowing users to import and work with notebooks created in these environments.
- Syntax Highlighting: The notebook interface features syntax highlighting, enhancing code readability and writability by distinguishing different parts of the code syntax.
- Integrated Help: LabPlot offers integrated help for CAS systems and programming languages, including features for downloading, searching, and navigating documentation, facilitating user learning and utilization of underlying system features.
Working with Computational Notebooks
- Launching a Notebook: To begin, users select the desired programming language or CAS from within LabPlot, opening a new notebook interface where they can write and execute code.
- Executing Code: Code execution is straightforward; users can select code and press the execution button or use a keyboard shortcut to run the code. The computation results are displayed directly below the executed code, facilitating immediate visualization and analysis.
- Visualizing Data: After performing calculations, users can select the output variables as sources for plots within the notebook interface. LabPlot automatically recognizes array-like data structures from supported languages, simplifying plot creation.
- Data Manipulation: Within the notebook, users can manipulate data using the syntax and functions of the chosen programming language. This includes filtering, sorting, aggregating, and transforming data before visualization.
- Saving and Sharing: Notebooks can be saved in the LabPlot project file format, facilitating easy sharing and collaboration. Users can also export notebooks to various formats for use in other applications or for sharing with others.
LabPlot as a Frontend to CAS
LabPlot can be used as a frontend to different open-source computer algebra systems (CAS) like Maxima, Octave, R, Scilab, and Sage or programming languages providing similar capabilities like Python and Julia. LabPlot recognizes different CAS variables holding array-like data and allows selecting them as a source for curves. So, instead of providing columns of a spreadsheet as the source for x- and y-data, the user provides the names of the corresponding CAS-variables. Currently supported CAS data containers are:
- Maxima lists
- Python lists, tuples and NumPy arrays
- Julia vectors and tuples
With this, powerful calculations carried out inside of different CAS environments can be combined with the user-friendly visualization and editing capabilities of LabPlot.
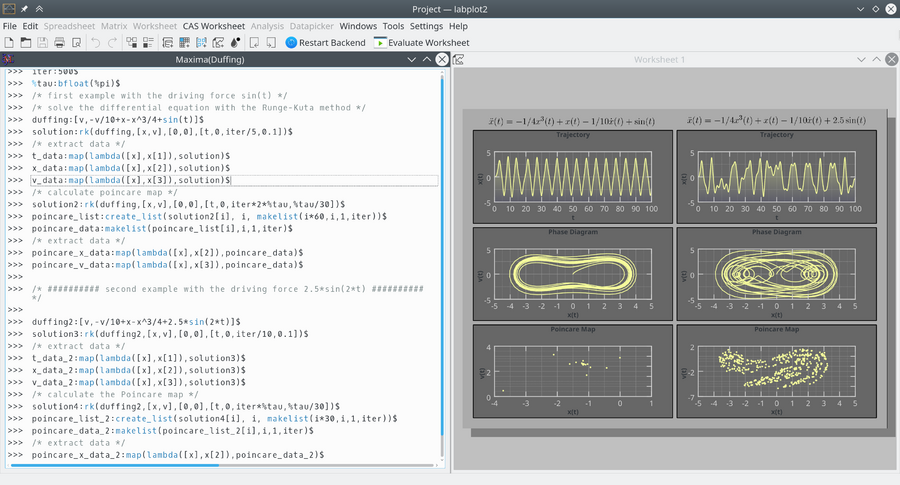
Maxima session exploring the chaotic dynamics of the Duffing oscillator. The forced oscillator's differential equation is solved using Maxima, and the results are visualized using LabPlot. Plots include the oscillator's trajectory, phase space, and Poincaré map, showcasing the system's complex behavior.
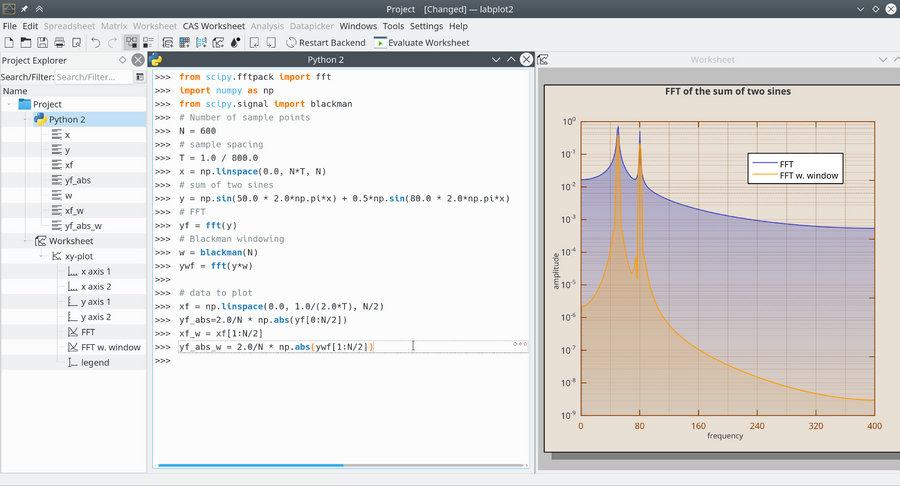
Python session analyzing the effect of Blackman windowing on the Fourier transform. It demonstrates how windowing can enhance the clarity of frequency components in signal processing, with plots showing the Fourier transform before and after applying the Blackman window.
See Also
See the video on how to use Computational Notebooks in LabPlot.
{{#ev:youtube|8lDQStVDevw|800|center}}
