KmPlot/de

Home » Applications » Education » de

KmPlot zeichnet die Grafen zu mathematischen Funktionen. Es gehört zum KDE Education Project.

Grafen einiger trigonometrischer Funktionen

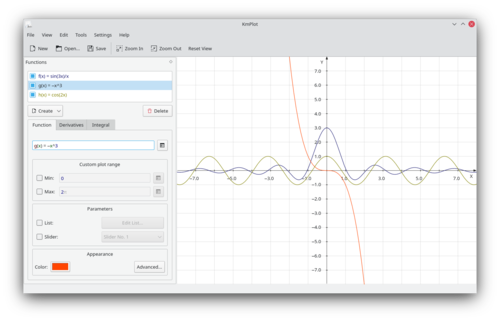
KmPlot besitzt einen mächtigen Parser, der die mathematischen Ausdrücke auswertet. Die Ausdrucke zeichnen sich durch hohe Präzision und korrekte metrische Skalierung der Achsen aus, was vor allem für Arbeitsblätter im Mathematik- oder naturwissenschaftlichen Unterricht nützlich ist.

Das Programm zeichnet mehrere Grafen in ein Koordinatensystem. Die Funktionsterme können zu neuen Funktionen kombiniert werden. KmPlot unterstützt auch die Darstellung von Kurvenscharen. Man kann den Parameter mit einem Schieberegler verändern und seinen Einfluss auf den Kurvenverlauf untersuchen.

Features

• mächtiger Parser für mathematische Ausdrücke
• präzise metrische Ausdrucke
• verschiedene Arten die Funktion zu definieren:
  • kartesisch
  • parametrisch
  • Gleichung in Polarkoordinaten
  • implizite Gleichung
  • Differenzialgleichung
• detaillierte Darstellungsoptionen (Linienstil, Achsen, Gitter)
• Export nach Bitmap- (BMP und PNG) und skalierbaren Vektorformaten (SVG)
• Speichern und Öffnen der kompletten Sitzung im XML-Format
• Trace-Modus: Ein Fadenkreuz folgt dem Kurvenverlauf, die Koordinaten werden in der Statuszeile angezeigt
• Vergrößern und Verkleinern
• die Grafen der ersten und zweiten Ableitung sowie der einer Integralfunktion können zusätzlich gezeichnet werden
• Benutzer definierte Konstanten und Parameterwerte
• diverse Hilfsmittel:
  • Näherungsweise Bestimmung von Hoch- und Tiefpunkten
  • Fläche unter dem Graphen auf einem Intervall bestimmen

Beispielgrafen

x(t)=0.5(t-2sin t) y(t)=2(1-2cos t)	rf(x)=x
x(t)=5sin(3t) y(t)=3cos(5t)	f(x)=3sin x g(x)=5cos(2x-pi/2) h(x)=f(x)+g(x)

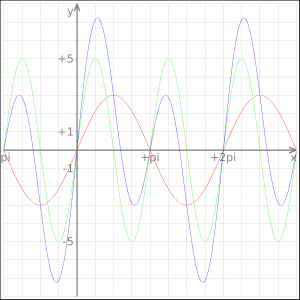
Ausführlichere Beispiele

• Using Sliders

Dokumentation

• KmPlot Handbuch