KmPlot/Using Sliders/de: Difference between revisions
< KmPlot
Pipesmoker (talk | contribs) (Created page with "Als nächstes lass uns untersuchen, wie weit ein Geschoss geworfen maximal werden kann, wenn man den Abwurfwinkel variiert. Wir verwenden eine parametrisierte Darstellung mit ein...") |
Pipesmoker (talk | contribs) (Created page with "* Definiere eine Konstante v_0 für die Anfangsgeschwindigkeit. * Erstelle eine parametrische Zeichnung. * Gib die folgenden Gleichungen ein: {{Input|1=<nowiki>f_x(t,α) = v_0∙...") |
||
| Line 22: | Line 22: | ||
Als nächstes lass uns untersuchen, wie weit ein Geschoss geworfen maximal werden kann, wenn man den Abwurfwinkel variiert. Wir verwenden eine parametrisierte Darstellung mit einem zusätzlichen Parameter, dem Winkel. | Als nächstes lass uns untersuchen, wie weit ein Geschoss geworfen maximal werden kann, wenn man den Abwurfwinkel variiert. Wir verwenden eine parametrisierte Darstellung mit einem zusätzlichen Parameter, dem Winkel. | ||
* | * Definiere eine Konstante v_0 für die Anfangsgeschwindigkeit. | ||
* | * Erstelle eine parametrische Zeichnung. | ||
* | * Gib die folgenden Gleichungen ein: {{Input|1=<nowiki>f_x(t,α) = v_0∙cos(α)∙t | ||
f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2</nowiki>}} | f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2</nowiki>}} | ||
Now you can move the slider and see how the distance depends on the parameter value. | Now you can move the slider and see how the distance depends on the parameter value. | ||
Revision as of 19:44, 11 October 2010
Ein besonderes Merkmal von KmPlot ist die Veranschaulichung der Wirkung eines Parameters auf den Kurvernverlauf einer Funktion.
Verschieben der Sinuskurve
Lass uns die Sinuskurve nach links und rechts verschieben:
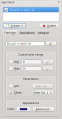
- Erstelle eine neue kartesische Zeichnung.
- Wähle die Option und wähle den aus der Liste aus.
- Damit die verfügbaren Schieberegler sichtbar werden, wähle im Menü aus.
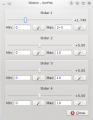
Nun kannst du den Schieberegler bewegen und beobachten, wie der Wert des Parameters die Position der Kurve beeinflusst.
- Bildschirmschnappschüsse
-
Eingabe
-
Regler anzeigen im Ansicht-Menü
-
Schieberegler-Fenster
Wurfparabel
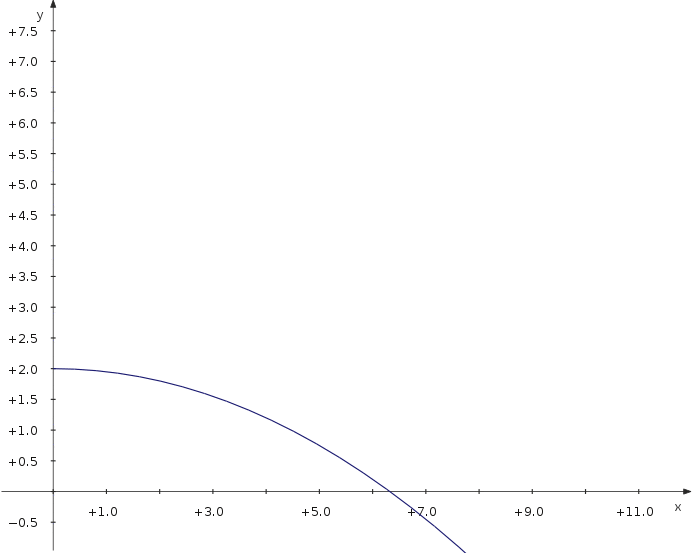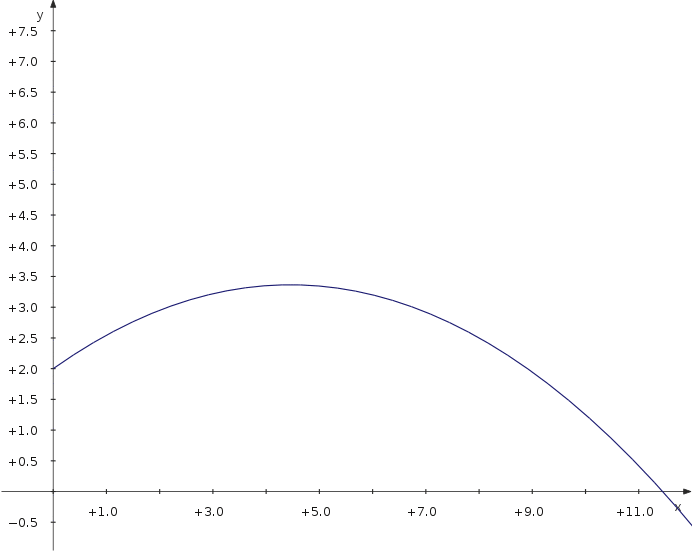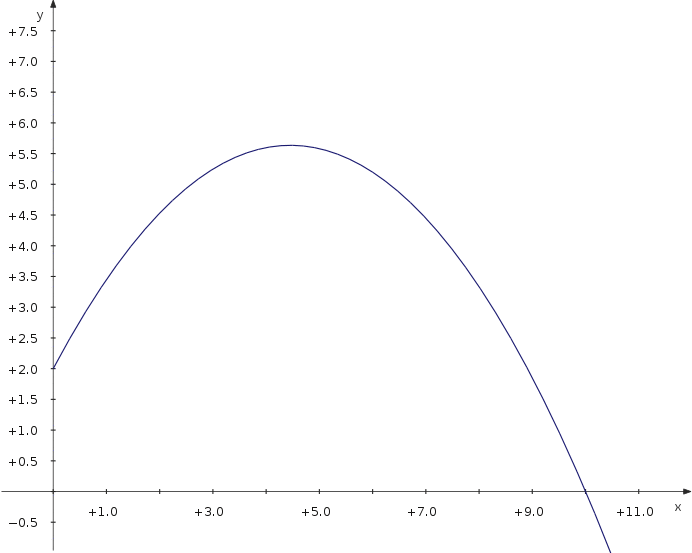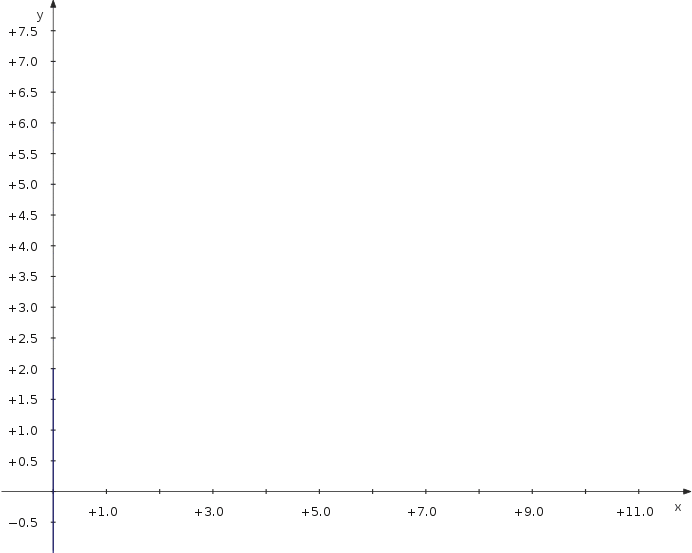
Als nächstes lass uns untersuchen, wie weit ein Geschoss geworfen maximal werden kann, wenn man den Abwurfwinkel variiert. Wir verwenden eine parametrisierte Darstellung mit einem zusätzlichen Parameter, dem Winkel.
- Definiere eine Konstante v_0 für die Anfangsgeschwindigkeit.
- Erstelle eine parametrische Zeichnung.
- Gib die folgenden Gleichungen ein:
f_x(t,α) = v_0∙cos(α)∙t f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2
Now you can move the slider and see how the distance depends on the parameter value.