KmPlot/Using Sliders/uk

Однією з основних можливостей KmPlot є можливість візуалізації впливу параметрів на графік функції.

Пересування графіка синуса

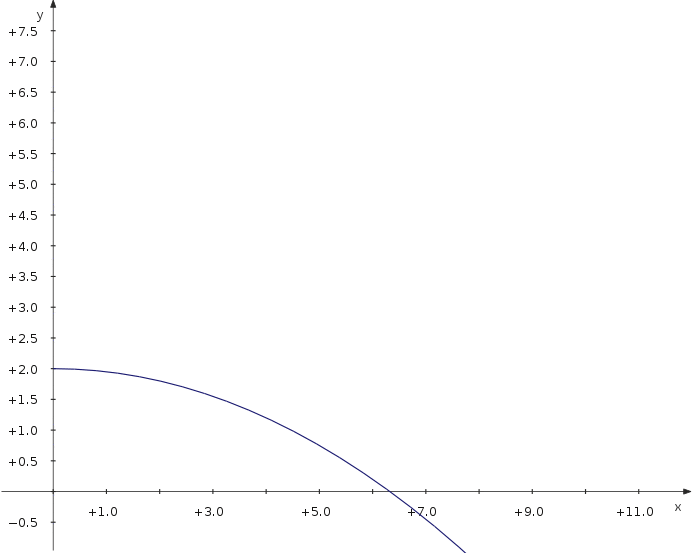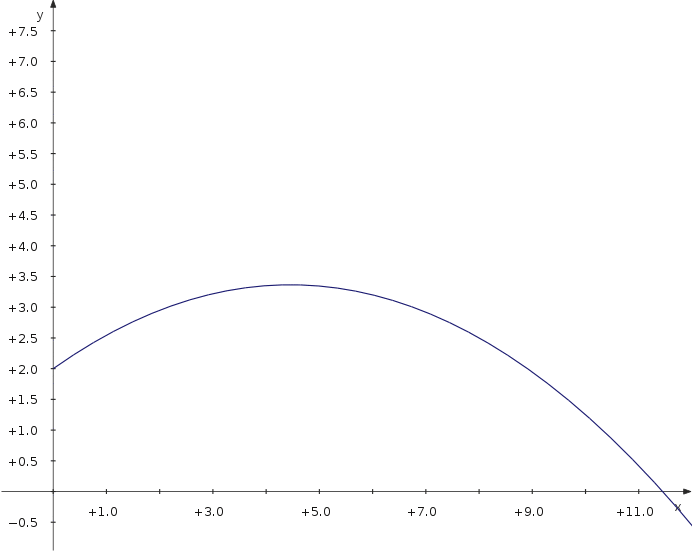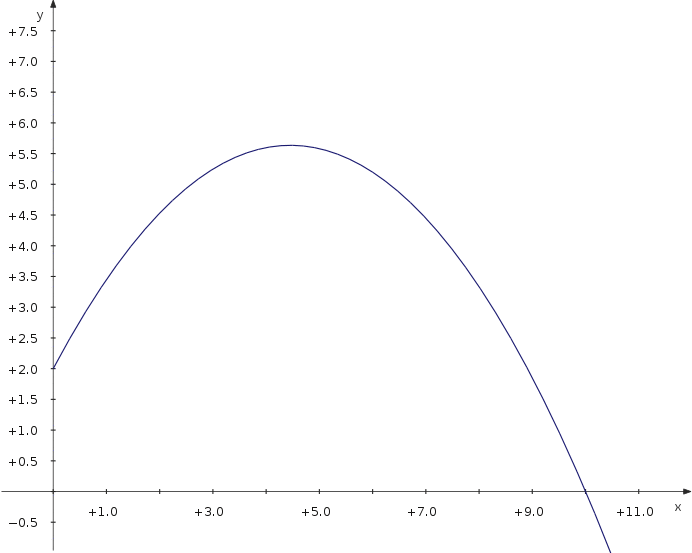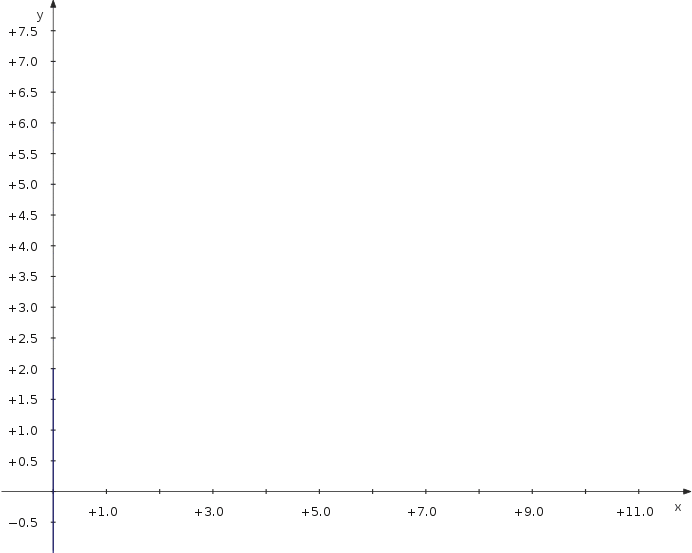
Давайте навчимося пересувати графік синуса ліворуч і праворуч:

• Створіть новий графік у прямокутній декартовій системі координат.
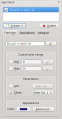
• Введіть рівняння кривої

  f(x,a) = sin(x-a)

• Позначте пункт Повзунок і виберіть Повзунок No. 1 зі спадного списку.
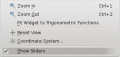
• Щоб зробити повзунки видимими, позначте пункт Перегляд -> Показати повзунки

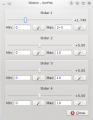
Now you can move the slider and see how the parameter value modifies the position of the curve.

• Screenshots
• 
  Input
• 
  Show sliders option
• 
  Slider window

Trajectory of a Projectile

Now let's have a look at the maximum distance of a projectile thrown with different angles. We use a parametric plot depending on an additional parameter which is the angle.

• Define a contant v_0 for the starting velocity.
• Create a new parametric plot
• Enter the equations

  f_x(t,α) = v_0∙cos(α)∙t
  f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2

• Check the Slider option and choose Slider No. 1 from the drop down list.
• To make the available sliders visible, check View -> Show Sliders

Now you can move the slider and see how the distance depends on the parameter value.