Digikam/AspectRatios/it: Difference between revisions
No edit summary |
No edit summary |
||
| Line 8: | Line 8: | ||
Ecco come farli. | Ecco come farli. | ||
Scegli l'immagine e premi <keycap>F4</keycap> o fai clic destro sull'immagine e scegli <menuchoice>Modifica</menuchoice>. Nella finestra dell'editor vai sulla barra del menu e fai clic su <menuchoice>Trasforma -> Taglia alle proporzioni</menuchoice>, comparirà questa finestra. | Scegli l'immagine e premi <keycap>F4</keycap> o fai clic destro sull'immagine e scegli <menuchoice>Modifica</menuchoice>. Nella finestra dell'editor vai sulla barra del menu e fai clic su <menuchoice>Trasforma -> Taglia alle proporzioni</menuchoice>, comparirà questa finestra. | ||
Revision as of 18:49, 22 February 2011
Effettuare tagli secondo proporzioni in digiKam
Trascritto dal blog di Mohamed Malik, 21 febbraio 2011
Ogni singolo schermo ha una proporzione, cioè un rapporto tra la larghezza e l'altezza. DigiKam può effettuare tagli conformi a queste molto facilmente. È molto utile se stai creando sfondi ed immagini che debbano adattarsi ad una determinata proporzione. Personalmente utilizzo questa funzionalità quando carico i miei sfondi su kde-look.
Ecco come farli.
Scegli l'immagine e premi F4 o fai clic destro sull'immagine e scegli . Nella finestra dell'editor vai sulla barra del menu e fai clic su , comparirà questa finestra.
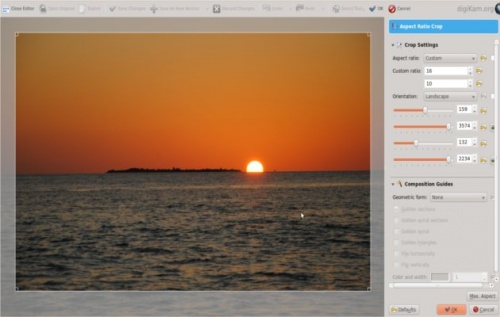
Lo strumento offre le seguenti proporzioni predefinite:
- 1:1
- 3:2
- 4:3
- 5:4
- 7:5
- 10:7 & 5:8
Offre anche un'opzione chiamata Rapporto aureo... Non ho ancora capito cosa fa o cosa significa! [1]
Offre anche la possibilità di personalizzare le proporzioni. Puoi quindi scegliere la proporzione che preferisci.
Dopo aver scelto una proporzione, prendi il piccolo quadrato che vedi sugli angoli dell'area evidenziata e spostalo sulla parte dell'immagine che vuoi tagliare. Qualsiasi area selezionerai, avrà le proporzioni da te specificate.
Note
- ↑ Una spiegazione del rapporto aureo è disponibile sul sito Maths is Fun
