KmPlot/Using Sliders/da: Difference between revisions
< KmPlot
(Importing a new version from external source) |
(Importing a new version from external source) |
||
| Line 23: | Line 23: | ||
Lad os nu se på den maksimale afstand for et projektil, som kastes med forskellige vinkler. Vi bruger et partametrisk plot, som afhænger af en ekstra parameter, som er vinklen. | Lad os nu se på den maksimale afstand for et projektil, som kastes med forskellige vinkler. Vi bruger et partametrisk plot, som afhænger af en ekstra parameter, som er vinklen. | ||
* | * Definer en konstant v_0 for starthastigheden. | ||
* | * Lav et parametrisk plot | ||
* | * Skriv ligningen {{Input|1=<nowiki>f_x(t,α) = v_0∙cos(α)∙t | ||
f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2</nowiki>}} | f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2</nowiki>}} | ||
* | * Markér tilvalget <menuchoice>Skyder</menuchoice> og vælg <menuchoice>Skyder nr. 1</menuchoice> fra dropnedfeltet. | ||
* | * For at gøre de tilgængelige skydere synlige, så vælg menuen <menuchoice>Vis -> Vis skydere</menuchoice> | ||
Now you can move the slider and see how the distance depends on the parameter value. | Now you can move the slider and see how the distance depends on the parameter value. | ||
Revision as of 16:46, 13 October 2010
En vigtig funktion i KmPlot er at visualisere parametres betydning for en funktions graf.
Bevæg en sinuskurve
Lad os se, hvordan man kan bevæge en sinuskurve til venstre og højre:
- Lav et Cartesisk plot.
- Skriv ligningen
f(x,a) = sin(x-a)
- Markér tilvalget og vælg fra dropnedfeltet.
- For at gøre de tilgængelige skydere synlige, så vælg menuen
Nu kan du trække skyderen frem og tilbage og se, hvordan parameterværdien påvirker kurvens position.
- Screenshots
-
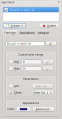
Input
-
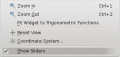
Menuen Vis skydere
-
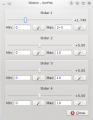
Skydervinduet
Et projektils bane
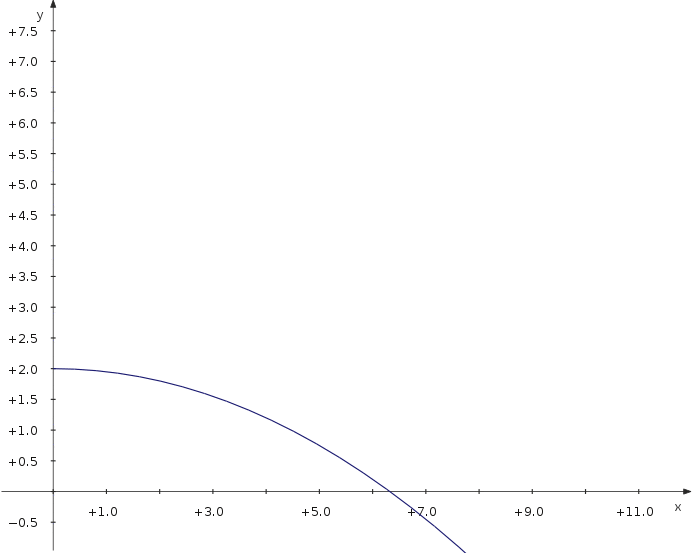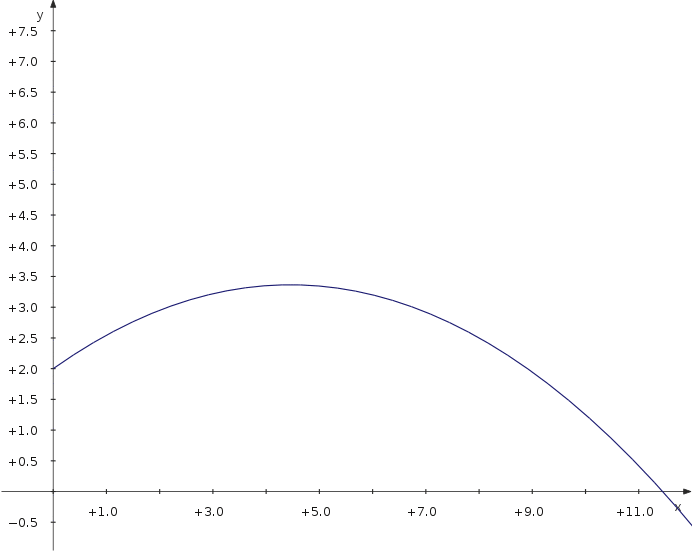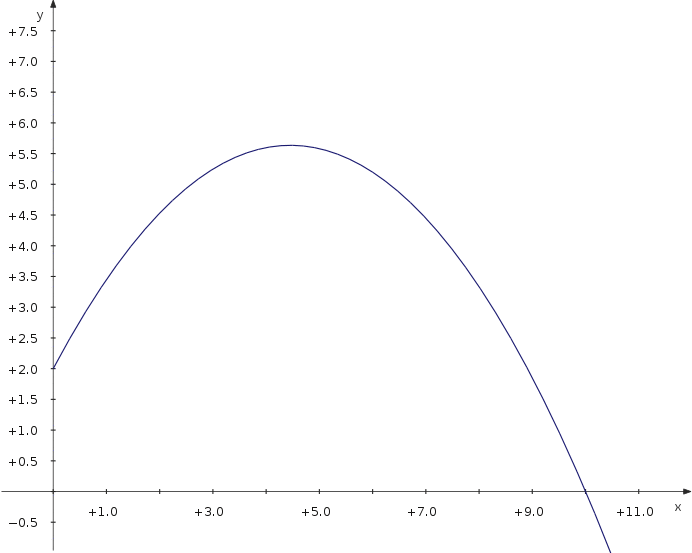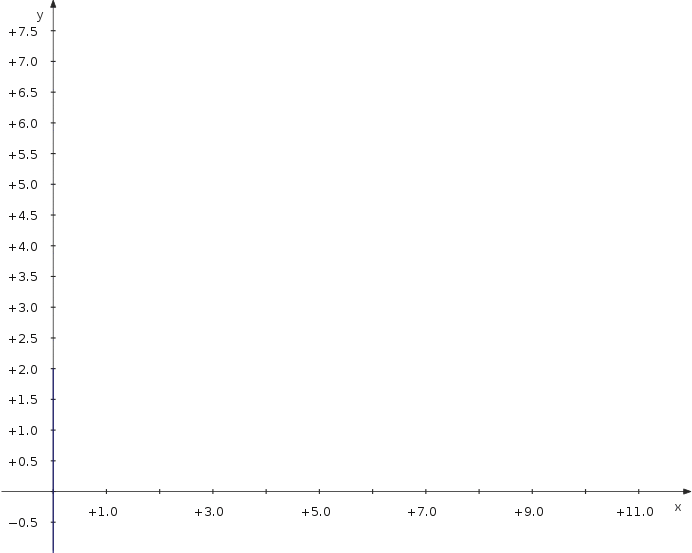
Lad os nu se på den maksimale afstand for et projektil, som kastes med forskellige vinkler. Vi bruger et partametrisk plot, som afhænger af en ekstra parameter, som er vinklen.
- Definer en konstant v_0 for starthastigheden.
- Lav et parametrisk plot
- Skriv ligningen
f_x(t,α) = v_0∙cos(α)∙t f_y(t,α) = 2+v_0∙sin(α)∙t−5∙t^2
- Markér tilvalget og vælg fra dropnedfeltet.
- For at gøre de tilgængelige skydere synlige, så vælg menuen
Now you can move the slider and see how the distance depends on the parameter value.