Kdenlive/Підручник/Переходи/Афінний
Афінний перехід
Виконує обертання зображення у просторі, перекошування та викривлення зображення.
Визначає анімовані афінні перетворення за ключовими кадрами із можливостями розчинення зображення.
In many applications, this transition can be used instead of a Composite transition and this provides a workaround to the composite transition "green tinge" bug reported by some. (Mantis #2759)
Приклад 1
{{#ev:youtube|hylowKurZaw}}
Розчинення за допомогою афінного переходу
Щоб додати розчинення, змініть рівень непрозорості до нуля відсотків.
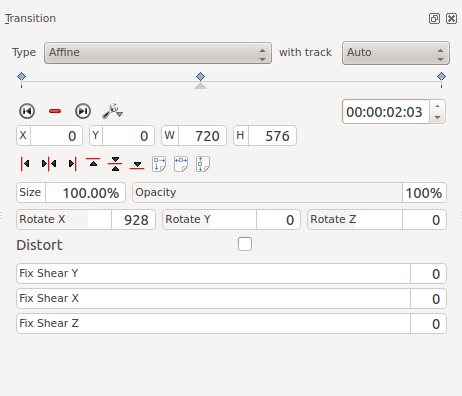
Обертання за допомогою афінного перерходу
Для обертання зображення додайте ключовий кадр і введіть значення кута обертання. Одиницями запису є десяті частки градуса (тобто 900 означає обертання на 90 градусів).
За допомогою параметра Обертання навколо X можна обертати кадр у площині екрана.
Параметри Обертання навколо Y та Обертання навколо Z створюють ілюзію обертання у просторі, якщо використовувати їх динамічно із ключовими кадрами — див. наведений нижче приклад.
Подібний ефект можна створити за допомогою ефекту Обертати (за ключовими кадрами) з групи ефектів обрізання та перетворення.
Приклад 2 — обертання за Y
{{#ev:youtube|IAWMIL7c9K4}}
Цей приклад створено за допомогою 3 ключових кадрів. Нижче показано другий ключовий кадр із значенням параметра Обертання навколо Y рівним 180O (=180 градусів). Для першого і третього ключових кадрів встановлено нульове значення параметра Обертання навколо Y.
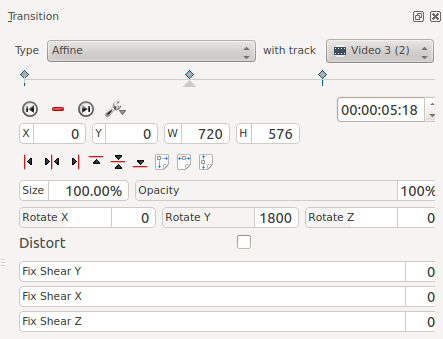
Відмінністю між пунктами Обертання навколо Y та Обертання навколо Z полягає у тому, що видиме обертання для пункту Обертання навколо Y виконується навколо горизонтальної вісі, а обертання для пункту Обертання навколо Z виконується навколо вертикальної вісі.
