KAlgebra/Homework/uk: Difference between revisions
No edit summary |
Created page with "Цією функцією можна скористатися так:
{{Input |<nowiki>Temp_ost2(4180,40,15,1925,30,70)
</nowiki>}}
{{Output |<nowiki>finalTemp2(4,180, 40, 15,..." |
||
| (14 intermediate revisions by 2 users not shown) | |||
| Line 109: | Line 109: | ||
===Приклад з однаковими матеріалами, але різними об’ємами та температурами=== | ===Приклад з однаковими матеріалами, але різними об’ємами та температурами=== | ||
Давайте знайдеом температуру суміші 40 літрів води з температурою 15°C та 30 літрів води з температурою 70°C? | Давайте знайдеом температуру суміші 40 літрів води з температурою 15°C та 30 літрів води з температурою 70°C? | ||
Скористаємося законом збереження енергії. Ми знаємо, енергія суміші є сумою енергій складових, отже (літерою Q ми позначили внутрішню енергію):<br /> | Скористаємося законом збереження енергії. Ми знаємо, енергія суміші є сумою енергій складових, отже (літерою Q ми позначили внутрішню енергію):<br /> | ||
:U<sub>сум</sub> = U1 + U2 | :U<sub>сум</sub> = U1 + U2 | ||
Внутрішня енергія є добутком теплоємності при сталому об’ємі на об’єм і на температуру:<br /> | |||
:U = C*V*T | :U = C*V*T | ||
Отже C<sub>ост</sub>*V<sub>ост</sub>*T<sub>ост</sub> = C1*V1*T1 + C2*V2*T2 | |||
Оскільки теплоємності є однаковими, на них можна скоротити. Остаточний об’єм дорівнюватиме сумі двох початкових об’ємів:<br /> | |||
:(V1+V2)*T<sub> | :(V1+V2)*T<sub>ост</sub> = V1*T1 + V2*T2 | ||
:: | ::або | ||
:T<sub> | :T<sub>ост</sub> = (V1*T1 + V2*T2)/(V1+V2) | ||
Тепер ми можемо або безпосередньо ввести значення у '''KAlgebra''': | |||
{{Input |<nowiki>(40*15 + 30*70)/(40 + 30) | {{Input |<nowiki>(40*15 + 30*70)/(40 + 30) | ||
</nowiki>}} | </nowiki>}} | ||
{{Output |<nowiki>(40*15+30*70)/(40+30) | {{Output |<nowiki>(40*15+30*70)/(40+30) | ||
=38.5714</nowiki>}} | =38.5714</nowiki>}} | ||
і отримати остаточну температуру, або створити функцію, якщо обчислення треба буде повторити: | |||
{{Input |<nowiki> | {{Input |<nowiki>Temp_ost:=(v1,t1,v2,t2)->(v1*t1 + v2*t2)/(v1+v2)</nowiki>}} | ||
Створеною функцією можна скористатися ось так: | |||
{{Input |<nowiki> | {{Input |<nowiki>Temp_ost(40,15,30,70) | ||
</nowiki>}} | </nowiki>}} | ||
{{Output |<nowiki> | {{Output |<nowiki>Temp_ost(40, 15, 30, 70) | ||
=38.5714</nowiki>}} | =38.5714</nowiki>}} | ||
=== | ===Приклад з двома різними рідинами=== | ||
Нехай тепер маємо дві рідини з різними теплоємностями, зокрема 4180 Дж/(л*К) для першої рідини (вода) та 1925 Дж/(л*К) для другої (етиловий спирт). | |||
Повернімося до рівняння:<br /> | |||
:C<sub> | :C<sub>ост</sub>*V<sub>ост</sub>*T<sub>ост</sub> = C1*V1*T1 + C2*V2*T2 | ||
Остаточна темлоємність буде середньою зваженою величиною відносно теплоємностей першої і другої рідин за об’ємом (оскільки це теплоємність при сталому об’ємі, а не при сталій масі чи молярності):<br /> | |||
:C<sub> | :C<sub>ост</sub> = (C1*V1 + C2*V2)/V<sub>ост</sub> | ||
Підставляючи це співвідношення до попереднього рівняння, ми отримаємо:<br /> | |||
:(C1*V1 + C2*V2)*T<sub> | :(C1*V1 + C2*V2)*T<sub>ост</sub> = C1*V1*T1 + C2*V2*T2 | ||
:: | ::або | ||
:T<sub> | :T<sub>ост</sub> = (C1*V1*T1 + C2*V2*T2)/(C1*V1 + C2*V2) | ||
Ми можемо або скористатися цією формулою безпосередньо: | |||
{{Input |<nowiki>(4180*40*15 + 1925*30*70)/(4180*40+1925*30) | {{Input |<nowiki>(4180*40*15 + 1925*30*70)/(4180*40+1925*30) | ||
</nowiki>}} | </nowiki>}} | ||
| Line 159: | Line 157: | ||
=29.1198</nowiki>}} | =29.1198</nowiki>}} | ||
Або створити функцію, якщо можливі подальші обчислення за цією формулою: | |||
{{Input |<nowiki> | {{Input |<nowiki>Temp_ost2:=(c1,v1,t1,c2,v2,t2)->(c1*v1*t1 + c2*v2*t2)/(c1*v1+c2*v2) | ||
</nowiki>}} | </nowiki>}} | ||
Цією функцією можна скористатися так: | |||
{{Input |<nowiki> | {{Input |<nowiki>Temp_ost2(4180,40,15,1925,30,70) | ||
</nowiki>}} | </nowiki>}} | ||
{{Output |<nowiki>finalTemp2(4,180, 40, 15, 1,925, 30, 70) | {{Output |<nowiki>finalTemp2(4,180, 40, 15, 1,925, 30, 70) | ||
=29.1198</nowiki>}} | =29.1198</nowiki>}} | ||
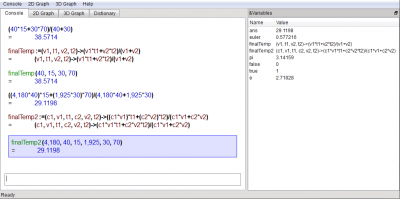
Знімок вікна '''KAlgebra''' після виконання обчислень: | |||
[[Image:KAlgebra-Fluids-Example-Screenshot.png|400px|center]] | [[Image:KAlgebra-Fluids-Example-Screenshot.png|400px|center]] | ||
[[Category:Освіта/uk]] | [[Category:Освіта/uk]] | ||
Latest revision as of 16:27, 29 April 2011
На цій сторінці наведено приклади застосування KAlgebra для розв’язання конкретних задач.
Приклад з комбінаторики
Нехай слід визначити кількість способів, якими можна розсадити 6 осіб (p1, p2 ... p6) навколо круглого столу з 6 стільцями.
Очевидно, можливі такі варіанти:
p1 p2 p3 p4 p5 p6 p1 p2 p3 p4 p6 p5 p1 p2 p3 p5 p4 p6 p1 p2 p3 p5 p6 p4
і так далі.
Можна зауважити, що останню позицію за столом можна заповнити лише у один спосіб, передостанню — у 2, далі — у 3, у 4, у 5, і нарешті у 6 способів. Отже загальну кількість варіантів можна визначити за допомогою простої формули:
6*5*4*3*2*1
Введемо цю формулу у консоль KAlgebra, і програма обчислить відповідь:
(((((1)*2)*3)*4)*5)*6 =720
Подібний розподіл значень за варіантами, де кількість значень дорівнює кількості варіантів називається «переставляннями».
Ви можете скористатися функцією KAlgebra для обчислення кількості таких переставлянь (ця функція називається «факторіал»):
factorial(6)
дасть нам
factorial(6) =720
Як бачите, ми отримали той самий результат.
Приклад з теорії ймовірностей
Визначимо ймовірність викинути певну грань гральної кістки.
Сприятливим для нас буде викидання відповідної грані, а несприятливим - викидання інших граней.
Отже, сприятливим буде лише один варіант із шести:
- ймовірність = кількість вибраних граней / загальна кількість граней = 1/6
Отже тепер ми знаємо, що ймовірність викидання певної грані кістки дорівнює 1/6.
Ви можете створити просту функцію у KAlgebra для отримання значення ймовірності за означенням:
jmovirnist:=(spryyatlyvi,zagalom)->spryyatlyvi/zagalom
Теорія чисел
Нехай нам потрібно визначити суму всіх цілих чисел у певному діапазоні, наприклад, від 1 до 100. Знаходження подібної суми без певної вправності у арифметиці (якщо ви знаєте потрібний прийом, це нескладно) справа доволі марудна.
У KAlgebra передбачено чудові можливості для виконання подібних обчислень. Віддайте у консолі такі команди:
sum(x: x=1..100)
в результаті отримаємо:
sum(x: x=1..100) = 5050
Вказана нами синтаксична конструкція призначена для виконання такої послідовності дій:
- 1. Обмежити діапазон значень x
- 2. Взяти перше значення x
- 3. Взяти друге значення x і додати попереднє значення x
- 4. Взяти третє значення x і додати попереднє значення x
- ...
- N. Взяти останнє значення x і додати останнє значення x
Розрахунок електричних ланцюгів
Приклад 1
Розглянемо простий елемент множення з двома вхідними портами та одним вихідним. Для визначення результату у KAlgebra можна скористатися таким кодом:
and(var1, var2)
Ми отримаємо результат логічного множення вхідних змінних.
Приклад 2
Розглянемо простий електричний ланцюг: джерело живлення з напругою 3 В та два елементи опору (R1 і R2) з’єднані паралельно з опором 3 кОм. Потрібно визначити струм, який проходитиме ланцюгом.
Для початку визначимо значення загального опору відповідно до такого закону:
- Rзаг = (1/R1 + 1/R2)-1
- I = U/Rзаг
Давайте створимо просту функцію у KAlgebra для виконання обчислень за вказаними формулами:
R_zag:=(R1,R2)->(1/R1+1/R2)^-1 I:=(U,R_zag)->U/R_zag
Подивимося, що у нас вийшло:
I(3, R_zag(3000, 3000))
I(3, R_zag(3 000, 3 000)) = 0,002
Теплопровідність
Приклад з однаковими матеріалами, але різними об’ємами та температурами
Давайте знайдеом температуру суміші 40 літрів води з температурою 15°C та 30 літрів води з температурою 70°C?
Скористаємося законом збереження енергії. Ми знаємо, енергія суміші є сумою енергій складових, отже (літерою Q ми позначили внутрішню енергію):
- Uсум = U1 + U2
Внутрішня енергія є добутком теплоємності при сталому об’ємі на об’єм і на температуру:
- U = C*V*T
Отже Cост*Vост*Tост = C1*V1*T1 + C2*V2*T2
Оскільки теплоємності є однаковими, на них можна скоротити. Остаточний об’єм дорівнюватиме сумі двох початкових об’ємів:
- (V1+V2)*Tост = V1*T1 + V2*T2
- або
- Tост = (V1*T1 + V2*T2)/(V1+V2)
Тепер ми можемо або безпосередньо ввести значення у KAlgebra:
(40*15 + 30*70)/(40 + 30)
(40*15+30*70)/(40+30) =38.5714
і отримати остаточну температуру, або створити функцію, якщо обчислення треба буде повторити:
Temp_ost:=(v1,t1,v2,t2)->(v1*t1 + v2*t2)/(v1+v2)
Створеною функцією можна скористатися ось так:
Temp_ost(40,15,30,70)
Temp_ost(40, 15, 30, 70) =38.5714
Приклад з двома різними рідинами
Нехай тепер маємо дві рідини з різними теплоємностями, зокрема 4180 Дж/(л*К) для першої рідини (вода) та 1925 Дж/(л*К) для другої (етиловий спирт).
Повернімося до рівняння:
- Cост*Vост*Tост = C1*V1*T1 + C2*V2*T2
Остаточна темлоємність буде середньою зваженою величиною відносно теплоємностей першої і другої рідин за об’ємом (оскільки це теплоємність при сталому об’ємі, а не при сталій масі чи молярності):
- Cост = (C1*V1 + C2*V2)/Vост
Підставляючи це співвідношення до попереднього рівняння, ми отримаємо:
- (C1*V1 + C2*V2)*Tост = C1*V1*T1 + C2*V2*T2
- або
- Tост = (C1*V1*T1 + C2*V2*T2)/(C1*V1 + C2*V2)
Ми можемо або скористатися цією формулою безпосередньо:
(4180*40*15 + 1925*30*70)/(4180*40+1925*30)
((4,180*40)*15+(1,925*30)*70)/(4,180*40+1,925*30) =29.1198
Або створити функцію, якщо можливі подальші обчислення за цією формулою:
Temp_ost2:=(c1,v1,t1,c2,v2,t2)->(c1*v1*t1 + c2*v2*t2)/(c1*v1+c2*v2)
Цією функцією можна скористатися так:
Temp_ost2(4180,40,15,1925,30,70)
finalTemp2(4,180, 40, 15, 1,925, 30, 70) =29.1198
Знімок вікна KAlgebra після виконання обчислень: