KAlgebra/Probabilities/uk

На цій сторінці наведено декілька прикладів використання KAlgebra для розв’язування задач теорії ймовірностей.

Вступ

Нехай ми ведемо гру 5 гральними кістками.

Теорія, яка лежить в основі гри

Спочатку проаналізуємо ситуацію з киданням однієї кістки:

Ймовірність отримати під час викидання будь-яке з чисел на кістці дорівнює 1/6 або 16,667%, оскільки ми маємо рівно 6 можливих результатів викидання і кожен з них є рівноймовірним з іншими.

Нижче наведено таблицю, де праворуч від числа на кістці записано ймовірність його випадання.

    1    16,667%
    2    16,667%
    3    16,667% 
    4    16,667% 
    5    16,667% 
    6    16,667% 

Якщо ми кидатимемо 2 кістки, розподіл ймовірностей, звичайно ж, зміниться:

    2    2,778%
    3    5,556%
    4    8,333%
    5    11,111%
    6    13,889%
    7    16,667%
    8    13,889%
    9    11,111%
    10   8,333%
    11   5,556%
    12   2,778%

Чому ж, на відміну від випадку з однією кісткою, маємо різні значення ймовірностей для кожного з чисел? Відповідь дуже проста. Розглянемо результат «4» і всі комбінації з двох натуральних чисел, які у сумі дають 4:

       1+3 = 4
   3+1 = 4
   2+2 = 4

Таким чином, нам слід додати ймовірності кожної з цих комбінацій, щоб отримати загальну ймовірність випадання суми 4. Ось результат:

  P(1,3) + P(3,1) + P(2,2) = 1/6 * 1/6 + 1/6 * 1/6 + 1/6 * 1/6 = 0,08333 = 8,333%

Отже, якщо у нас буде 5 кісток, нам доведеться додавати ймовірності для всіх варіантів чисел на 5 кістках, які у сумі дають потрібне нам число. Спосіб отримання ймовірностей сум для більшої кількості кісток є аналогічним.

Задача зі знаходження ймовірності

Розгляньмо задачу зі знаходження ймовірності випадання з п’яти кісток трьох з шістками.

Знайти цю ймовірність можна таким чином: ймовірність випадання шістки на одній кістці * ймовірність випадання шістки на ще одній кістці * ймовірність випадання шістки на ще одній кістці * ймовірність випадання не шістки на одній кістці * ймовірність випадання не шістки на ще одній кістці

Потрібна нам комбінація може бути такою: 6 6 6 2 3, або такою: 5 6 6 6 1. Отже нам слід врахувати те, що нас задовольнятиме будь-який порядок випадання кісток, аби лише серед них було рівно три шістки. Тому слід ввести до розрахунків біноміальні коефіцієнти. Обчислити біноміальний коефіцієнт з N по M у KAlgebra можна таким чином:

factorial(N) / (factorial(M) * factorial(N-M))

Це комбінаторне число, яке визначається такою формулою:

comb:=(N,M)->factorial(N) / (factorial(M) * factorial(N-M))

Отже, біноміальний коефіцієнт для 3 чисел у 5 позиціях буде таким:

comb(5,3)

=	10

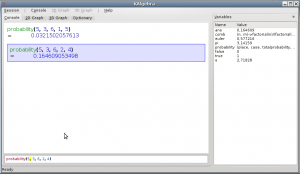
Отже наша функція набуде такого остаточного вигляду:

(comb(5, 3)*(1/6)*(1/6)*(1/6)*(5/6)*(5/6))

=	0.0321502

We can now define a simple function to get the result:

binomial:=(b, p, k)->(comb(b, k)*p^k)*(1-p)^(b-k)

So now:

binomial(5, 1/6,3)

=	0.0321502

It's the probability on 5 extraction to get 3 identical number where the probability of each card is 1/6 and the negative probability is 5/6

We can notice that the sum of probabilities is 1:

sum(binomial(5,1/6,t):t=0..5)

=	1

We can think that the probability progress until the maximum value and then it decrease constantly as it has progressed. So we can see that the distribution of numbers among the extraction is like a bell, this kind of distribution is called a binomial distribution.

So now we understand that the game is non balanced, there are probabilities better than other so who choose the best can win easily.

The only way to have a fair game is to gambling with only one die because each face has 1/6 of probability. Another type of equiprobal chances are the launch of a coin where each face is 1/2 of probability.

A simple way where a player can win is to improve the probability on a face so it will be unbalanced, for istance the bank in a game can put a small load on the face with '6' so the probabilities change and the dice now became:

0.15 	 1
0.15	 2
0.15	 3
0.15	 4
0.15	 5
0.25	 6

So now if we roll the 5 dices with this probability and we want 3 '6' to win the total probability is:

binomial(5,0.25,3)

=	0.087890625

Snapshot of KAlgebra window doing calculations about probabilities

Реалістичний приклад

There are two person, the bank and the player. Let's say they have 5 dices and the entrance fee for player is 1$. We can create a game like this:

0 to 1 times dice with '6': player loses 1$ with the fee

2 to 3 times dice with '6': player win 1$ with the fee

4 times dice with '6': player win 175$ with the fee

5 times dice with '6': player win 375$ with the fee

Кількість шісток	Виграш або програш
0	-1$
1	-1$
2	1$
3	1$
4	175$
5	375$

Let's calculate the probability:

Probability for player:

The player can win only with 2-3 times 6, 4 times 6 or 5 times 6, so if we want to process the probability with KAlgebra it will be:

binomial(5,1/6,2)+binomial(5,1/6,3)+binomial(5,1/6,4)+binomial(5,1/6,5)

=	0.196244855967

Probability for bank:

The bank can win only with 0-1 times 6, so if we want to process the probability with KAlgebra it will be:

binomial(5,1/6,0)+binomial(5,1/6,1)

=	0.803755144033

We now want to see if player and bank are balanced, We create a function win(x), that create a correspondence between values and prizes:

win:=x->piecewise { x=0 ? -1, x=1 ? -1, x=2 ? 1, x=3 ? 1, x=4 ? 175, x=5 ? 375, ? 0 }

Let's verify the expression with KAlgebra:

sum(win(x)*binomial(5,1/6,x): x=0..5)

=	-2.01227923213e-16

Результатом мав бути 0, але через похибки у внутрішньому представленні чисел у ком’ютері ми отримали лише близьке до нуля число.

Як бачимо, у цьому випадку маємо гру з нульовою сумою: ні гравець, ні казино нічого не виграють, якщо гра продовжуватиметься нескінченно довго.